Predicting pileups: Using ML to predict Chicago crash types
By Jeremy R. Winget in Blog
December 18, 2021
Wouldn’t it be great to know the chances of being injured or having your car totaled in a car accident before ever being involved in the accident? If you live in a less densely populated area, this question might not be very interesting. But if you live in a big city, like Chicago, you might be a little more concerned about this. By identifying factors that predict these bad accidents, we might be able to develop low cost interventions or redesign the environment to reduce the frequency of these types of accidents, which can translate to lives and money saved. So in this post, we’ll use machine learning to predict which traffic crashes in Chicago, IL, result in injuries and/or the vehicle being towed based on situational features (e.g., posted speed limit, lighting conditions, road surface condition, etc.) that are likely known before the crash occurred.
Traffic crash data were imported from the Chicago Data Portal using the RSocrata package. The City of Chicago also has data sets related to the vehicles and people involved in these crashes, but to keep things simple for now, let’s focus on a few situational factors related to the crash, all of which can be found in the main data set.
These data show information about each traffic crash on city streets within the City of Chicago and under the jurisdiction of the Chicago Police Department. Many of the variables (e.g. street conditions, weather conditions, etc.) are recorded by the reporting officer and are based on the best available information at the time, but according to the Chicago Data Portal, these data may disagree with other posted information. As such, data are subject to change based on new information.
Import data
set.seed(20211218)
library(RSocrata)
library(tidyverse)
library(lubridate)
library(janitor)
library(tidymodels)
library(vip)
library(skimr, include.only = "skim")
# data pulled at time of post; new cases likely added to data portal since then
crashes <- read.socrata(
"https://data.cityofchicago.org/resource/85ca-t3if.csv", # url of data set
app_token = Sys.getenv("rsocrata_token") # my personal creds
) %>%
clean_names() %>%
select(
crash_type, crash_date, posted_speed_limit, traffic_control_device,
device_condition, weather_condition, lighting_condition, first_crash_type,
trafficway_type, alignment, roadway_surface_cond, road_defect, prim_contributory_cause
) %>%
mutate(
crash_date = ymd_hms(crash_date),
date = as_date(crash_date)
) %>%
select(!crash_date)
The goal here is to build a model that predicts whether a crash will result in someone being injured and/or the vehicle being towed using the crash_type variable in the crashes data set.
From the variables listed in the
Traffic Crash data set, let’s select some that are likely to have been known before the crash occurred. For example, lighting_condition is a variable that records the light condition at the time of the crash. This situational factor is likely to be known (e.g., observed by the driver, reported by others prior to the crash, etc.) before an accident occurs. At the very least, this information has a higher chance of being known prior to a crash compared to something like injuries_total. injuries_total is a variable that records the total number of people who sustained an injury as a result of the accident. Since this is a consequence of a crash, this information can only known after the crash occurs.
With this logic, let’s focus on the following variables from the initial Traffic Crash data set:
| Column name | Description | Type |
|---|---|---|
| crash_date | Date and time of crash as entered by the reporting officer | Date/Time |
| posted_speed_limit | Posted speed limit, as determined by reporting officer | Numeric |
| traffic_control_device | Traffic control device present at crash location, as determined by reporting officer | Factor |
| device_condition | Condition of traffic control device, as determined by reporting officer | Factor |
| weather_condition | Weather condition at time of crash, as determined by reporting officer | Factor |
| lighting_condition | Light condition at time of crash, as determined by reporting officer | Factor |
| first_crash_type | Type of first collision in crash | Factor |
| trafficway_type | Trafficway type, as determined by reporting officer | Factor |
| alignment | Street alignment at crash location, as determined by reporting officer | Factor |
| roadway_surface_cond | Road surface condition, as determined by reporting officer | Factor |
| road_defect | Road defects, as determined by reporting officer | Factor |
| prim_contributory_cause | The factor which was most significant in causing the crash, as determined by officer judgment | Factor |
Data exploration & cleaning
Now that we have some idea of what we’ll be looking at in our model, let’s get some impressions of the data and see if anything needs to be cleaned up before going further.
glimpse(crashes)
Rows: 571,184
Columns: 13
$ crash_type <chr> "NO INJURY / DRIVE AWAY", "INJURY AND / OR TOW…
$ posted_speed_limit <int> 30, 30, 30, 30, 35, 30, 30, 30, 20, 20, 30, 30…
$ traffic_control_device <chr> "NO CONTROLS", "STOP SIGN/FLASHER", "TRAFFIC S…
$ device_condition <chr> "NO CONTROLS", "FUNCTIONING PROPERLY", "FUNCTI…
$ weather_condition <chr> "CLEAR", "CLEAR", "CLEAR", "CLEAR", "CLEAR", "…
$ lighting_condition <chr> "DARKNESS, LIGHTED ROAD", "DAYLIGHT", "DAYLIGH…
$ first_crash_type <chr> "REAR END", "ANGLE", "TURNING", "ANGLE", "TURN…
$ trafficway_type <chr> "ONE-WAY", "DIVIDED - W/MEDIAN (NOT RAISED)", …
$ alignment <chr> "STRAIGHT AND LEVEL", "STRAIGHT AND LEVEL", "S…
$ roadway_surface_cond <chr> "DRY", "DRY", "DRY", "DRY", "DRY", "DRY", "UNK…
$ road_defect <chr> "NO DEFECTS", "UNKNOWN", "NO DEFECTS", "NO DEF…
$ prim_contributory_cause <chr> "IMPROPER OVERTAKING/PASSING", "FAILING TO RED…
$ date <date> 2019-08-21, 2016-09-20, 2018-04-16, 2018-04-2…
The first thing to note is that there are 571426 observations with 13 columns in the crashes data set. And other than some potential capitalization issues with the strings, there doesn’t seem to be any obvious issues with the way the data are formatted. We’ll come back to this, but for now, let’s check for missing data.
colSums(is.na(crashes))
crash_type posted_speed_limit traffic_control_device
0 0 0
device_condition weather_condition lighting_condition
0 0 0
first_crash_type trafficway_type alignment
0 0 0
roadway_surface_cond road_defect prim_contributory_cause
0 0 0
date
0
Great, no missing data! This will simplify data preparation later on. Next, we should examine the frequency counts of the variables we’ll use to predict the outcome class.
var_freq <- function(df) {
map(names(df), ~ count(df, .data[[.x]]))[1:12]
}
var_freq(crashes)
[[1]]
crash_type n
1 INJURY AND / OR TOW DUE TO CRASH 146704
2 NO INJURY / DRIVE AWAY 424722
[[2]]
posted_speed_limit n
1 0 6967
2 1 37
3 2 22
4 3 135
5 4 2
6 5 3982
7 6 7
8 7 2
9 9 94
10 10 12618
11 11 8
12 12 3
13 14 3
14 15 20184
15 16 1
16 18 2
17 20 23046
18 22 2
19 23 1
20 24 29
21 25 35213
22 26 2
23 29 1
24 30 420252
25 31 2
26 32 15
27 33 11
28 34 13
29 35 39110
30 36 5
31 38 2
32 39 62
33 40 5287
34 45 3513
35 49 1
36 50 133
37 55 545
38 60 32
39 63 1
40 65 12
41 70 3
42 99 66
[[3]]
traffic_control_device n
1 BICYCLE CROSSING SIGN 17
2 DELINEATORS 191
3 FLASHING CONTROL SIGNAL 182
4 LANE USE MARKING 1226
5 NO CONTROLS 328889
6 NO PASSING 26
7 OTHER 3505
8 OTHER RAILROAD CROSSING 137
9 OTHER REG. SIGN 591
10 OTHER WARNING SIGN 513
11 PEDESTRIAN CROSSING SIGN 275
12 POLICE/FLAGMAN 206
13 RAILROAD CROSSING GATE 374
14 RR CROSSING SIGN 66
15 SCHOOL ZONE 188
16 STOP SIGN/FLASHER 56828
17 TRAFFIC SIGNAL 158633
18 UNKNOWN 18773
19 YIELD 806
[[4]]
device_condition n
1 FUNCTIONING IMPROPERLY 2913
2 FUNCTIONING PROPERLY 197610
3 MISSING 68
4 NO CONTROLS 332457
5 NOT FUNCTIONING 1854
6 OTHER 4442
7 UNKNOWN 31851
8 WORN REFLECTIVE MATERIAL 231
[[5]]
weather_condition n
1 BLOWING SAND, SOIL, DIRT 2
2 BLOWING SNOW 169
3 CLEAR 454044
4 CLOUDY/OVERCAST 16937
5 FOG/SMOKE/HAZE 858
6 FREEZING RAIN/DRIZZLE 701
7 OTHER 1732
8 RAIN 50003
9 SEVERE CROSS WIND GATE 116
10 SLEET/HAIL 736
11 SNOW 20386
12 UNKNOWN 25742
[[6]]
lighting_condition n
1 DARKNESS 28092
2 DARKNESS, LIGHTED ROAD 124367
3 DAWN 9773
4 DAYLIGHT 370366
5 DUSK 17184
6 UNKNOWN 21644
[[7]]
first_crash_type n
1 ANGLE 61096
2 ANIMAL 400
3 FIXED OBJECT 26634
4 HEAD ON 4918
5 OTHER NONCOLLISION 1828
6 OTHER OBJECT 5501
7 OVERTURNED 345
8 PARKED MOTOR VEHICLE 132917
9 PEDALCYCLIST 8437
10 PEDESTRIAN 13077
11 REAR END 133128
12 REAR TO FRONT 4027
13 REAR TO REAR 886
14 REAR TO SIDE 2413
15 SIDESWIPE OPPOSITE DIRECTION 8319
16 SIDESWIPE SAME DIRECTION 87334
17 TRAIN 36
18 TURNING 80130
[[8]]
trafficway_type n
1 ALLEY 9369
2 CENTER TURN LANE 4602
3 DIVIDED - W/MEDIAN (NOT RAISED) 98035
4 DIVIDED - W/MEDIAN BARRIER 33689
5 DRIVEWAY 1953
6 FIVE POINT, OR MORE 574
7 FOUR WAY 23286
8 L-INTERSECTION 80
9 NOT DIVIDED 253000
10 NOT REPORTED 214
11 ONE-WAY 75267
12 OTHER 15948
13 PARKING LOT 39919
14 RAMP 1793
15 ROUNDABOUT 139
16 T-INTERSECTION 4950
17 TRAFFIC ROUTE 436
18 UNKNOWN 6310
19 UNKNOWN INTERSECTION TYPE 1293
20 Y-INTERSECTION 569
[[9]]
alignment n
1 CURVE ON GRADE 853
2 CURVE ON HILLCREST 272
3 CURVE, LEVEL 4335
4 STRAIGHT AND LEVEL 557037
5 STRAIGHT ON GRADE 7225
6 STRAIGHT ON HILLCREST 1704
[[10]]
roadway_surface_cond n
1 DRY 430091
2 ICE 3943
3 OTHER 1375
4 SAND, MUD, DIRT 241
5 SNOW OR SLUSH 20443
6 UNKNOWN 39264
7 WET 76069
[[11]]
road_defect n
1 DEBRIS ON ROADWAY 478
2 NO DEFECTS 472661
3 OTHER 3214
4 RUT, HOLES 4855
5 SHOULDER DEFECT 1212
6 UNKNOWN 86671
7 WORN SURFACE 2335
[[12]]
prim_contributory_cause
1 ANIMAL
2 BICYCLE ADVANCING LEGALLY ON RED LIGHT
3 CELL PHONE USE OTHER THAN TEXTING
4 DISREGARDING OTHER TRAFFIC SIGNS
5 DISREGARDING ROAD MARKINGS
6 DISREGARDING STOP SIGN
7 DISREGARDING TRAFFIC SIGNALS
8 DISREGARDING YIELD SIGN
9 DISTRACTION - FROM INSIDE VEHICLE
10 DISTRACTION - FROM OUTSIDE VEHICLE
11 DISTRACTION - OTHER ELECTRONIC DEVICE (NAVIGATION DEVICE, DVD PLAYER, ETC.)
12 DRIVING ON WRONG SIDE/WRONG WAY
13 DRIVING SKILLS/KNOWLEDGE/EXPERIENCE
14 EQUIPMENT - VEHICLE CONDITION
15 EVASIVE ACTION DUE TO ANIMAL, OBJECT, NONMOTORIST
16 EXCEEDING AUTHORIZED SPEED LIMIT
17 EXCEEDING SAFE SPEED FOR CONDITIONS
18 FAILING TO REDUCE SPEED TO AVOID CRASH
19 FAILING TO YIELD RIGHT-OF-WAY
20 FOLLOWING TOO CLOSELY
21 HAD BEEN DRINKING (USE WHEN ARREST IS NOT MADE)
22 IMPROPER BACKING
23 IMPROPER LANE USAGE
24 IMPROPER OVERTAKING/PASSING
25 IMPROPER TURNING/NO SIGNAL
26 MOTORCYCLE ADVANCING LEGALLY ON RED LIGHT
27 NOT APPLICABLE
28 OBSTRUCTED CROSSWALKS
29 OPERATING VEHICLE IN ERRATIC, RECKLESS, CARELESS, NEGLIGENT OR AGGRESSIVE MANNER
30 PASSING STOPPED SCHOOL BUS
31 PHYSICAL CONDITION OF DRIVER
32 RELATED TO BUS STOP
33 ROAD CONSTRUCTION/MAINTENANCE
34 ROAD ENGINEERING/SURFACE/MARKING DEFECTS
35 TEXTING
36 TURNING RIGHT ON RED
37 UNABLE TO DETERMINE
38 UNDER THE INFLUENCE OF ALCOHOL/DRUGS (USE WHEN ARREST IS EFFECTED)
39 VISION OBSCURED (SIGNS, TREE LIMBS, BUILDINGS, ETC.)
40 WEATHER
n
1 486
2 72
3 803
4 1238
5 764
6 6450
7 10785
8 213
9 4132
10 2514
11 277
12 2837
13 18131
14 3658
15 1083
16 1982
17 1684
18 24758
19 62495
20 58791
21 630
22 24242
23 21609
24 27301
25 18880
26 19
27 30637
28 47
29 7318
30 76
31 3467
32 213
33 1348
34 1500
35 250
36 403
37 214923
38 2972
39 3382
40 9056
Looks like there are some issues that need to be addressed here! First, the responses that are coded for some variables don’t make sense. For example, posted_speed_limit has 6967 recorded observations for a posted speed limit of 0 mph. Clearly, this is not a legitimate posted speed limit within the City of Chicago (as much as it may feel like it on the Dan Ryan at 5pm). There are some other odd speed limits recorded for this variable as well.
Another issue these frequency counts reveal is that many of the levels within a variable could be grouped together. For example, prim_contributory_cause makes a distinction between disregarding road markings, stop signs, traffic signals, yield signs, and other traffic signs. Instead, these levels could be grouped into a single level called “disregarding signs/markings”.
So, let’s address each of these problems by cleaning up the levels for each variable. And while we’re at it, let’s clean up the format of all of the strings so there is a consistent style (i.e., lower case).
crashes <- crashes %>%
mutate(
across(where(is.character), ~ str_to_lower(.)),
traffic_control_device = case_when(
traffic_control_device == "railroad crossing gate" |
traffic_control_device == "other railroad crossing" |
traffic_control_device == "rr crossing sign" ~ "rr crossing",
traffic_control_device == "bicycle crossing sign" |
traffic_control_device == "pedestrian crossing sign" |
traffic_control_device == "school zone" ~ "pedestrian signs",
traffic_control_device == "flashing control signal" ~ "stop sign/flasher",
traffic_control_device == "no passing" ~ "other warning sign",
TRUE ~ traffic_control_device
),
device_condition = case_when(
device_condition == "missing" ~ "no controls",
device_condition == "worn reflective material" |
device_condition == "not functioning" ~ "functioning improperly",
TRUE ~ device_condition
),
weather_condition = case_when(
weather_condition == "blowing sand, soil, dirt" |
weather_condition == "severe cross wind gate" |
weather_condition == "blowing snow" ~ "blowing debris",
weather_condition == "freezing rain/drizzle" |
weather_condition == "sleet/hail" ~ "sleet/hail/freezing rain",
TRUE ~ weather_condition
),
prim_contributory_cause = case_when(
prim_contributory_cause == "disregarding other traffic signs" |
prim_contributory_cause == "disregarding road markings" |
prim_contributory_cause == "disregarding stop sign" |
prim_contributory_cause == "disregarding traffic signals" |
prim_contributory_cause == "disregarding yield sign" |
prim_contributory_cause == "passing stopped school bus" ~ "disregarding signs/markings",
prim_contributory_cause == "distraction - from inside vehicle" |
prim_contributory_cause == "distraction - from outside vehicle" |
prim_contributory_cause == "distraction - other electronic device (navigation device, dvd player, etc.)" |
prim_contributory_cause == "cell phone use other than texting" |
prim_contributory_cause == "texting" ~ "distraction",
prim_contributory_cause == "had been drinking (use when arrest is not made)" |
prim_contributory_cause == "under the influence of alcohol/drugs (use when arrest is effected)" ~ "under the influence",
prim_contributory_cause == "obstructed crosswalks" |
prim_contributory_cause == "vision obscured (signs, tree limbs, buildings, etc.)" ~ "obstructions",
prim_contributory_cause == "bicycle advancing legally on red light" |
prim_contributory_cause == "motorcycle advancing legally on red light" ~ "bike/motorcycle advancing legally on red light",
prim_contributory_cause == "animal" |
prim_contributory_cause == "evasive action due to animal, object, nonmotorist" ~ "evasive action",
prim_contributory_cause == "exceeding authorized speed limit" |
prim_contributory_cause == "exceeding safe speed for conditions" ~ "speeding",
TRUE ~ prim_contributory_cause
),
across(where(is_character), ~ as_factor(.))
)
Great! Now, the data are clean, and we can start thinking about how to set up the model. Let’s take a look at the current data summary.
skim(crashes)
Table: Table 1: Data summary
| Name | crashes |
| Number of rows | 571184 |
| Number of columns | 13 |
| _______________________ | |
| Column type frequency: | |
| Date | 1 |
| factor | 11 |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: Date
| skim_variable | n_missing | complete_rate | min | max | median | n_unique |
|---|---|---|---|---|---|---|
| date | 0 | 1 | 2013-03-03 | 2021-12-16 | 2019-04-04 | 2360 |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| crash_type | 0 | 1 | FALSE | 2 | no : 424559, inj: 146625 |
| traffic_control_device | 0 | 1 | FALSE | 13 | no : 328744, tra: 158581, sto: 56983, unk: 18764 |
| device_condition | 0 | 1 | FALSE | 5 | no : 332373, fun: 197537, unk: 31837, fun: 4996 |
| weather_condition | 0 | 1 | FALSE | 9 | cle: 453842, rai: 49987, unk: 25729, sno: 20386 |
| lighting_condition | 0 | 1 | FALSE | 6 | day: 370247, dar: 124277, dar: 28081, unk: 21635 |
| first_crash_type | 0 | 1 | FALSE | 18 | rea: 133081, par: 132866, sid: 87296, tur: 80093 |
| trafficway_type | 0 | 1 | FALSE | 20 | not: 252898, div: 97994, one: 75242, par: 39894 |
| alignment | 0 | 1 | FALSE | 6 | str: 556802, str: 7219, cur: 4334, str: 1704 |
| roadway_surface_cond | 0 | 1 | FALSE | 7 | dry: 429895, wet: 76044, unk: 39245, sno: 20443 |
| road_defect | 0 | 1 | FALSE | 7 | no : 472466, unk: 86626, rut: 4855, oth: 3213 |
| prim_contributory_cause | 0 | 1 | FALSE | 26 | una: 214837, fai: 62463, fol: 58770, not: 30619 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| posted_speed_limit | 0 | 1 | 28.33 | 6.37 | 0 | 30 | 30 | 30 | 99 | ▁▇▁▁▁ |
And, let’s take a closer look at the dependent variable, crash_type.
crashes %>%
count(crash_type) %>%
mutate(prop = n / sum(n))
crash_type n prop
1 no injury / drive away 424559 0.7432964
2 injury and / or tow due to crash 146625 0.2567036
It looks like there might be a bit of imbalance in the data since the class proportions are skewed towards non-injury/drive-away (74.3%) crash types. Imbalance can sometimes lead to problems in an analysis, especially in severe cases of imbalance. Fortunately, there are a few approaches that try to mitigate this issue (e.g., themis). For now, let’s just analyze the data as is.
At this point, it would be helpful to know which variables in the crashes data set are associated with the different levels of the dependent variable, crash_type. One quick way of doing this for the numeric predictors is by using box plots.
crashes %>%
ggplot(aes(x = crash_type, y = posted_speed_limit, fill = crash_type)) +
geom_boxplot()
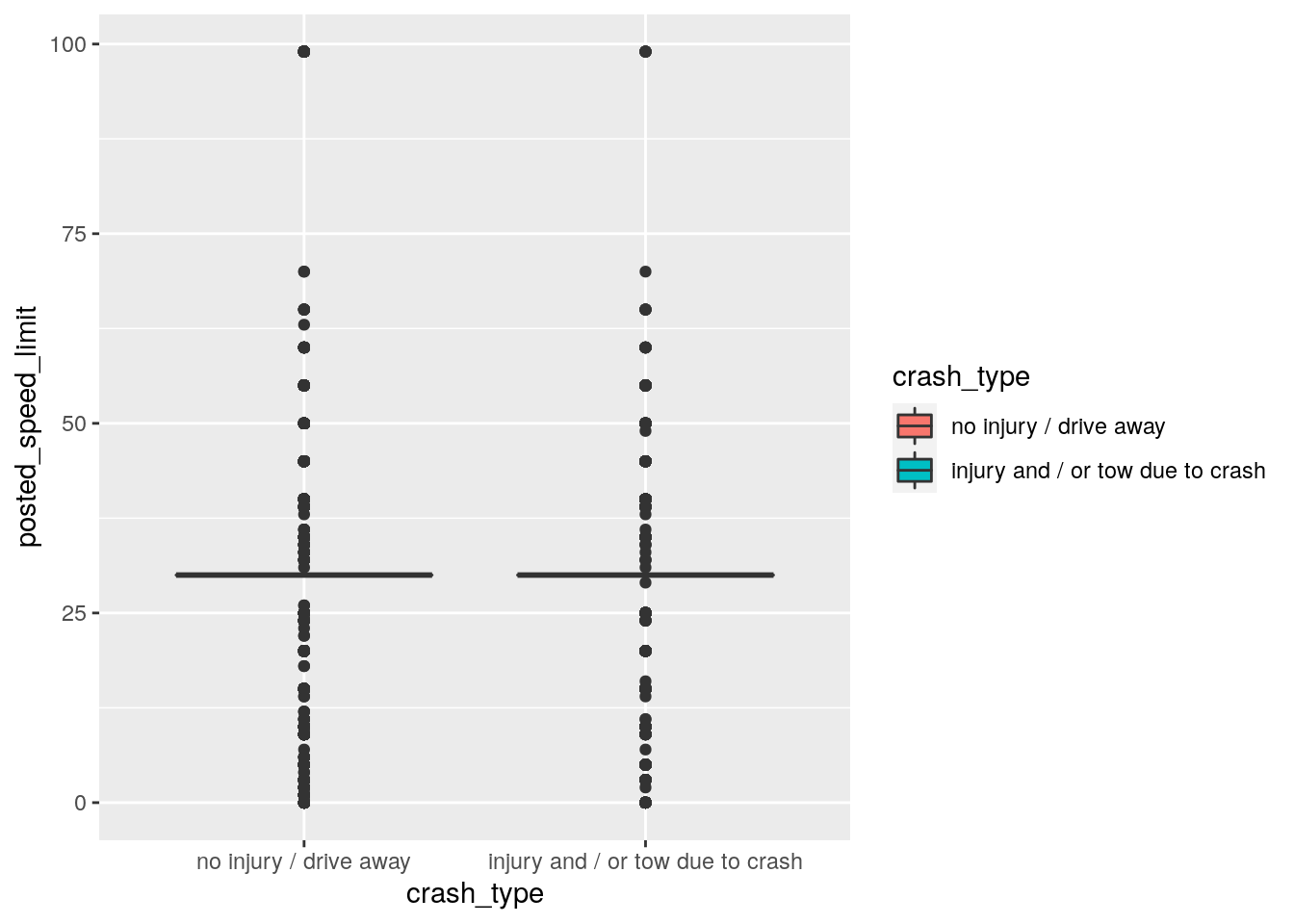
It looks like any differences between the crash_type levels are quite small for posted_speed_limit. So, maybe this variable won’t be so helpful in predicting injuries/towed crash types after all.
Next, let’s check the the relationship between the categorical variables and crash_type using simple counts. We’ll also filter for counts that are at least 1% of the total proportion of observations to get a better idea of the larger data patterns.
print_counts <- function(.y_var) {
y_var <- sym(.y_var)
crashes %>%
count(crash_type, {{y_var}}) %>%
group_by(crash_type) %>%
mutate(percent = round_half_up(n / sum(n) * 100, 2))
}
y_var <- crashes %>%
select(where(is.factor), -crash_type) %>%
variable.names()
map(y_var, print_counts) %>%
map(., ~ filter(., percent > 1))
[[1]]
# A tibble: 8 × 4
# Groups: crash_type [2]
crash_type traffic_control_device n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away no controls 256324 60.4
2 no injury / drive away stop sign/flasher 35711 8.41
3 no injury / drive away traffic signal 111530 26.3
4 no injury / drive away unknown 15550 3.66
5 injury and / or tow due to crash no controls 72420 49.4
6 injury and / or tow due to crash stop sign/flasher 21272 14.5
7 injury and / or tow due to crash traffic signal 47051 32.1
8 injury and / or tow due to crash unknown 3214 2.19
[[2]]
# A tibble: 7 × 4
# Groups: crash_type [2]
crash_type device_condition n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away no controls 258832 61.0
2 no injury / drive away functioning properly 134448 31.7
3 no injury / drive away unknown 24928 5.87
4 injury and / or tow due to crash no controls 73541 50.2
5 injury and / or tow due to crash functioning properly 63089 43.0
6 injury and / or tow due to crash functioning improperly 1690 1.15
7 injury and / or tow due to crash unknown 6909 4.71
[[3]]
# A tibble: 10 × 4
# Groups: crash_type [2]
crash_type weather_condition n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away clear 338172 79.6
2 no injury / drive away snow 15085 3.55
3 no injury / drive away rain 33841 7.97
4 no injury / drive away unknown 22999 5.42
5 no injury / drive away cloudy/overcast 11782 2.78
6 injury and / or tow due to crash clear 115670 78.9
7 injury and / or tow due to crash snow 5301 3.62
8 injury and / or tow due to crash rain 16146 11.0
9 injury and / or tow due to crash unknown 2730 1.86
10 injury and / or tow due to crash cloudy/overcast 5150 3.51
[[4]]
# A tibble: 12 × 4
# Groups: crash_type [2]
crash_type lighting_condition n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away darkness, lighted road 78019 18.4
2 no injury / drive away daylight 286739 67.5
3 no injury / drive away darkness 21017 4.95
4 no injury / drive away dusk 12700 2.99
5 no injury / drive away unknown 19373 4.56
6 no injury / drive away dawn 6711 1.58
7 injury and / or tow due to crash darkness, lighted road 46258 31.6
8 injury and / or tow due to crash daylight 83508 57.0
9 injury and / or tow due to crash darkness 7064 4.82
10 injury and / or tow due to crash dusk 4474 3.05
11 injury and / or tow due to crash unknown 2262 1.54
12 injury and / or tow due to crash dawn 3059 2.09
[[5]]
# A tibble: 18 × 4
# Groups: crash_type [2]
crash_type first_crash_type n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away rear end 106805 25.2
2 no injury / drive away angle 36442 8.58
3 no injury / drive away turning 55022 13.0
4 no injury / drive away parked motor vehicle 110650 26.1
5 no injury / drive away sideswipe same direction 77445 18.2
6 no injury / drive away fixed object 12861 3.03
7 no injury / drive away sideswipe opposite direction 6514 1.53
8 injury and / or tow due to crash rear end 26276 17.9
9 injury and / or tow due to crash angle 24628 16.8
10 injury and / or tow due to crash turning 25071 17.1
11 injury and / or tow due to crash parked motor vehicle 22216 15.2
12 injury and / or tow due to crash sideswipe same direction 9851 6.72
13 injury and / or tow due to crash pedestrian 11368 7.75
14 injury and / or tow due to crash fixed object 13761 9.39
15 injury and / or tow due to crash pedalcyclist 5793 3.95
16 injury and / or tow due to crash head on 2353 1.6
17 injury and / or tow due to crash other object 1777 1.21
18 injury and / or tow due to crash sideswipe opposite direction 1800 1.23
[[6]]
# A tibble: 19 × 4
# Groups: crash_type [2]
crash_type trafficway_type n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away one-way 60477 14.2
2 no injury / drive away divided - w/median (not rais… 69962 16.5
3 no injury / drive away divided - w/median barrier 21105 4.97
4 no injury / drive away not divided 189352 44.6
5 no injury / drive away parking lot 37295 8.78
6 no injury / drive away other 12187 2.87
7 no injury / drive away four way 11106 2.62
8 no injury / drive away unknown 5651 1.33
9 no injury / drive away alley 7504 1.77
10 injury and / or tow due to crash one-way 14765 10.1
11 injury and / or tow due to crash divided - w/median (not rais… 28032 19.1
12 injury and / or tow due to crash divided - w/median barrier 12571 8.57
13 injury and / or tow due to crash not divided 63546 43.3
14 injury and / or tow due to crash parking lot 2599 1.77
15 injury and / or tow due to crash other 3756 2.56
16 injury and / or tow due to crash t-intersection 2406 1.64
17 injury and / or tow due to crash four way 12166 8.3
18 injury and / or tow due to crash alley 1860 1.27
19 injury and / or tow due to crash center turn lane 1870 1.28
[[7]]
# A tibble: 5 × 4
# Groups: crash_type [2]
crash_type alignment n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away straight and level 416089 98
2 no injury / drive away straight on grade 4526 1.07
3 injury and / or tow due to crash straight and level 140713 96.0
4 injury and / or tow due to crash curve, level 2023 1.38
5 injury and / or tow due to crash straight on grade 2693 1.84
[[8]]
# A tibble: 8 × 4
# Groups: crash_type [2]
crash_type roadway_surface_cond n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away dry 319707 75.3
2 no injury / drive away unknown 34230 8.06
3 no injury / drive away snow or slush 15746 3.71
4 no injury / drive away wet 51021 12.0
5 injury and / or tow due to crash dry 110188 75.2
6 injury and / or tow due to crash unknown 5015 3.42
7 injury and / or tow due to crash snow or slush 4697 3.2
8 injury and / or tow due to crash wet 25023 17.1
[[9]]
# A tibble: 4 × 4
# Groups: crash_type [2]
crash_type road_defect n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away no defects 346415 81.6
2 no injury / drive away unknown 69629 16.4
3 injury and / or tow due to crash no defects 126051 86.0
4 injury and / or tow due to crash unknown 16997 11.6
[[10]]
# A tibble: 31 × 4
# Groups: crash_type [2]
crash_type prim_contributory_cause n percent
<fct> <fct> <int> <dbl>
1 no injury / drive away improper overtaking/passing 23620 5.56
2 no injury / drive away failing to reduce speed to avoid crash 14053 3.31
3 no injury / drive away disregarding signs/markings 7596 1.79
4 no injury / drive away failing to yield right-of-way 38742 9.13
5 no injury / drive away improper turning/no signal 13687 3.22
6 no injury / drive away unable to determine 172537 40.6
7 no injury / drive away not applicable 24582 5.79
8 no injury / drive away driving skills/knowledge/experience 14122 3.33
9 no injury / drive away improper backing 22880 5.39
10 no injury / drive away following too closely 48108 11.3
# … with 21 more rows
It looks like any differences between the two crash_type classes are small for alignment and weather_condition as well. However, because of the small differences across multiple levels of weather_condition, it’s tough to see if really there is a relationship there or not. Another way we can look for differences between two categorical variables is by plotting a heatmap of the frequency counts.
crashes %>%
ggplot(aes(crash_type, weather_condition)) +
geom_bin2d()
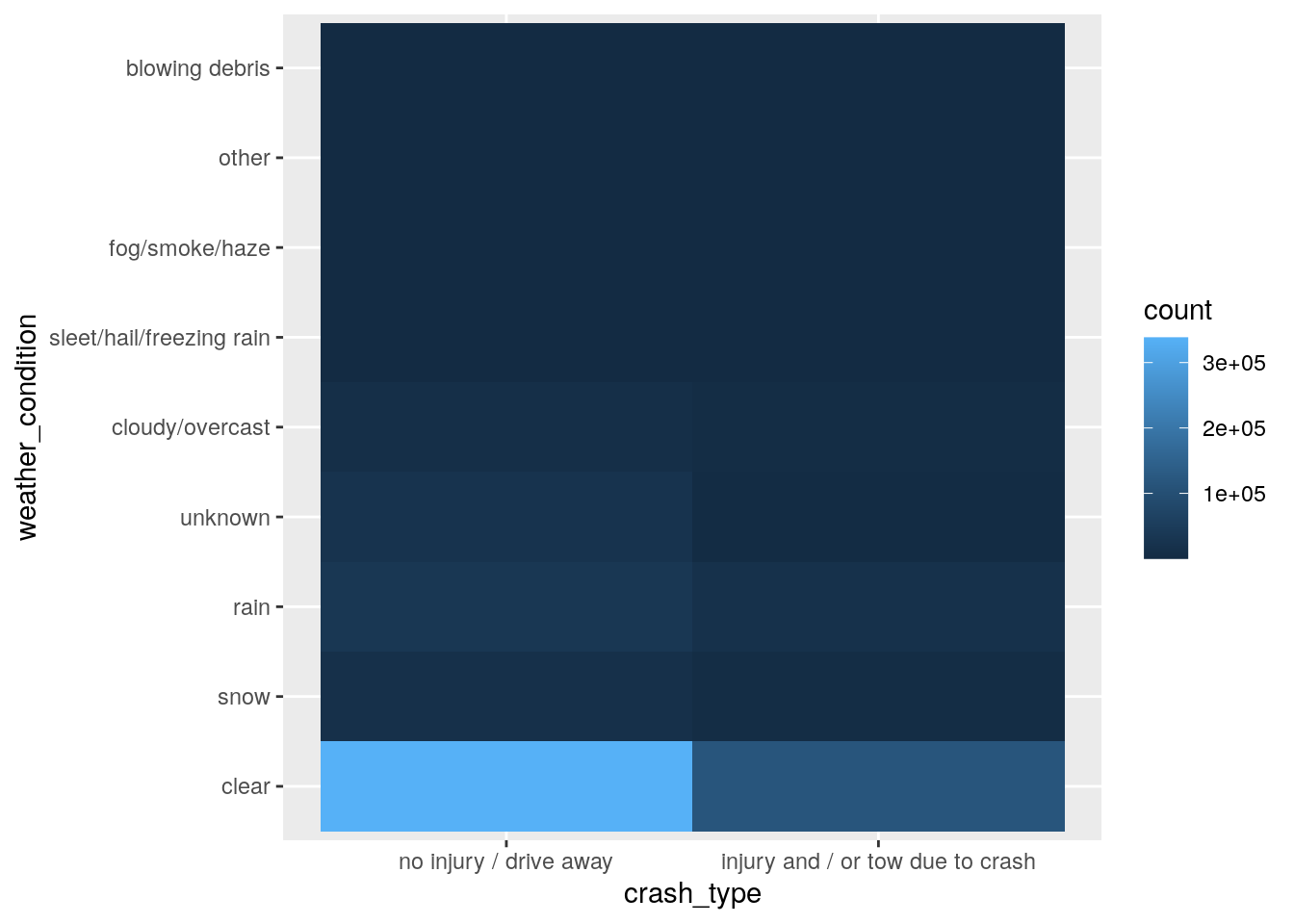
Although there are some differences, these appear to be pretty small. So, perhaps weather isn’t important for this model either.
Data preparation
Next, we’ll do a bit of preprocessing before training the models. This is where we’ll handle feature selection, data splitting, feature engineering, feature scaling, and creating the validation set (i.e., resampling).
The first thing we’ll do here is drop the variables that did not seem to have much of a relationship with crash_type during data exploration.
crashes <- select(crashes, -c(posted_speed_limit, weather_condition, alignment))
Next, let’s split the single data set into two: a training set and a testing set. A training data set is a data set of examples used during the learning process and is used to fit the models. A test data set is a data set that is independent of the training data set and is used to evaluate the performance of the final model. If a model fit to the training data set also fits the test data set well, we can be confident minimal overfitting has taken place. On the other hand, if the model seems to fit the training set better than the test set, we might have a case of overfitting.
For a data splitting strategy, let’s set aside 25% of the data for the test set. Since the outcome variable (crash_type) is somewhat imbalanced, we’ll also use a stratified random sample.
crash_split <- initial_split(crashes, strata = crash_type)
crash_train <- training(crash_split)
crash_test <- testing(crash_split)
Next, let’s create a base recipe for all models. Note the sequence of steps does matter here:
receipe():- Any variable on the left-hand side of the tilde (
~) is considered the model outcome (here,crash_type). The predictors of the model outcome appear on the right-hand side of the tilde. Here, we use the dot (.) to indicate all the other variables will be used as predictors. - A recipe is also associated with the data set used to create the model. This will usually be the training set, so
crash_trainhere.
- Any variable on the left-hand side of the tilde (
step_date(): Creates predictors for the year, month, and day of the week. Here, we’re selecting only the day of the week and month since there are limited observations for earlier years (e.g., 2013, 2014) in the data.step_rm(): Removes variables; here we use it to remove the original date variable since we no longer want it in the model.step_normalize(): Centers and scales numeric variables.step_dummy(): Converts characters or factors (i.e., nominal variables) into one or more numeric binary model terms for the levels of the original data.step_zv(): Removes indicator variables that only contain a single unique value (e.g. all zeros).
crash_recipe <- recipe(crash_type ~ ., data = crash_train) %>%
step_date(date, features = c("dow", "month")) %>%
step_rm(date) %>%
step_normalize(all_numeric_predictors(), -all_outcomes()) %>%
step_dummy(all_nominal_predictors(), -all_outcomes()) %>%
step_zv(all_predictors(), -all_outcomes())
Recall that we already partitioned our data set into a training set and test set. This lets us judge whether a given model will generalize well to new data. However, using only two partitions may be insufficient when doing many rounds of hyperparameter tuning. So, it’s usually a good idea to create a validation set as well. We’ll use k-fold cross validation to build a set of 5 validation folds with the function vfold_cv, and we’ll also use stratified sampling to maintain the outcome class proportions.
k-fold cross validation randomly allocates the 571184 observations in the training set to 5 groups of roughly equal size, called “folds”. For the first iteration of resampling, the first fold is held out for the purpose of measuring performance. The other 80% of the data are used to fit the model. This model, trained on the analysis set, is applied to the assessment set to generate predictions. Then, performance statistics are computed based on those predictions.
In this case, 5-fold cross validation iteratively moves through the folds and leaves a different 20% out each time for model assessment. At the end of this process, there are 5 sets of performance statistics that were created on 5 data sets that were not used in the modeling process. While 5 models were created, these are not used further; we do not keep the models themselves trained on these folds because their only purpose is calculating performance metrics. The final resampling estimates for the model are the averages of the performance statistics replicates.
crashes_vfold <- vfold_cv(crash_train, v = 5, strata = crash_type)
We will come back to the validation set after we specified the models.
Model 1: Logistic regression
All available models are listed at
https://www.tidymodels.org/find/parsnip/. Since the outcome variable (crash_type) is categorical, a logistic regression model is a good place to start. Let’s use a model that can perform feature selection during training. The
glmnet R package fits a generalized linear model via penalized maximum likelihood. This method of estimating the logistic regression slope parameters uses a penalty on the process so that less relevant predictors are driven towards a value of zero. One of the glmnet penalization methods, called the
lasso method, can set the predictor slopes to zero if a large enough penalty is used.
To specify a penalized logistic regression model that uses a feature selection penalty, let’s use the parsnip package with the glmnet engine.
lr_mod <- logistic_reg(penalty = tune(), mixture = 1) %>%
set_engine("glmnet") %>%
set_mode("classification")
We’ll set the penalty argument to tune() as a placeholder for now. This is a model hyperparameter that we will
tune to find the best value for making predictions with our data. Setting mixture to a value of 1 means the glmnet model will potentially remove irrelevant predictors and choose a simpler model (i.e., via least absolute shrinkage and selection operator).
Create the workflow
Now, let’s bundle the model and recipe into a single workflow() object to make management of the R objects easier.
lr_workflow <- workflow() %>%
add_model(lr_mod) %>%
add_recipe(crash_recipe)
Train and tune the model
Before we fit this model, we need to set up a grid of penalty values to tune. Since there is only one hyperparameter to tune here, we can set the grid up manually using a one-column tibble with 30 candidate values.
lr_reg_grid <- tibble(penalty = 10^seq(-4, -1, length.out = 30))
Now we can use the validation set (crashes_vfold) to estimate the performance of our models by fitting the models on each of the folds and storing the results.
Let’s use tune_grid() to train these penalized logistic regression models. This will fit our model to each resample and evaluate on the heldout set from each resample. We’ll also save the validation set predictions (using control_grid()) so that diagnostic information can be available after the model fit. The area under the ROC curve, precision, recall, and F1-Score metrics will be used to quantify how well the model performs across a continuum of event thresholds.
lr_res <- lr_workflow %>%
tune_grid(
crashes_vfold,
grid = lr_reg_grid,
control = control_grid(save_pred = TRUE),
metrics = metric_set(roc_auc, precision, recall, f_meas)
)
Evaluate the model
Let’s take a look at the performance for every single fold.
lr_res %>%
collect_metrics()
# A tibble: 120 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.0001 f_meas binary 0.873 5 0.000454 Preprocessor1_Model01
2 0.0001 precision binary 0.810 5 0.000335 Preprocessor1_Model01
3 0.0001 recall binary 0.947 5 0.000940 Preprocessor1_Model01
4 0.0001 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model01
5 0.000127 f_meas binary 0.873 5 0.000454 Preprocessor1_Model02
6 0.000127 precision binary 0.810 5 0.000335 Preprocessor1_Model02
7 0.000127 recall binary 0.947 5 0.000940 Preprocessor1_Model02
8 0.000127 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model02
9 0.000161 f_meas binary 0.873 5 0.000454 Preprocessor1_Model03
10 0.000161 precision binary 0.810 5 0.000335 Preprocessor1_Model03
# … with 110 more rows
This isn’t very helpful on it’s own. Let’s visualize the validation set metrics by plotting the area under the ROC curve against the range of penalty values.
lr_res %>%
collect_metrics() %>%
filter(`.metric` == "roc_auc") %>%
ggplot(aes(x = penalty, y = mean)) +
geom_point() +
geom_line() +
ylab("Area under the ROC Curve") +
scale_x_log10(labels = scales::label_number())
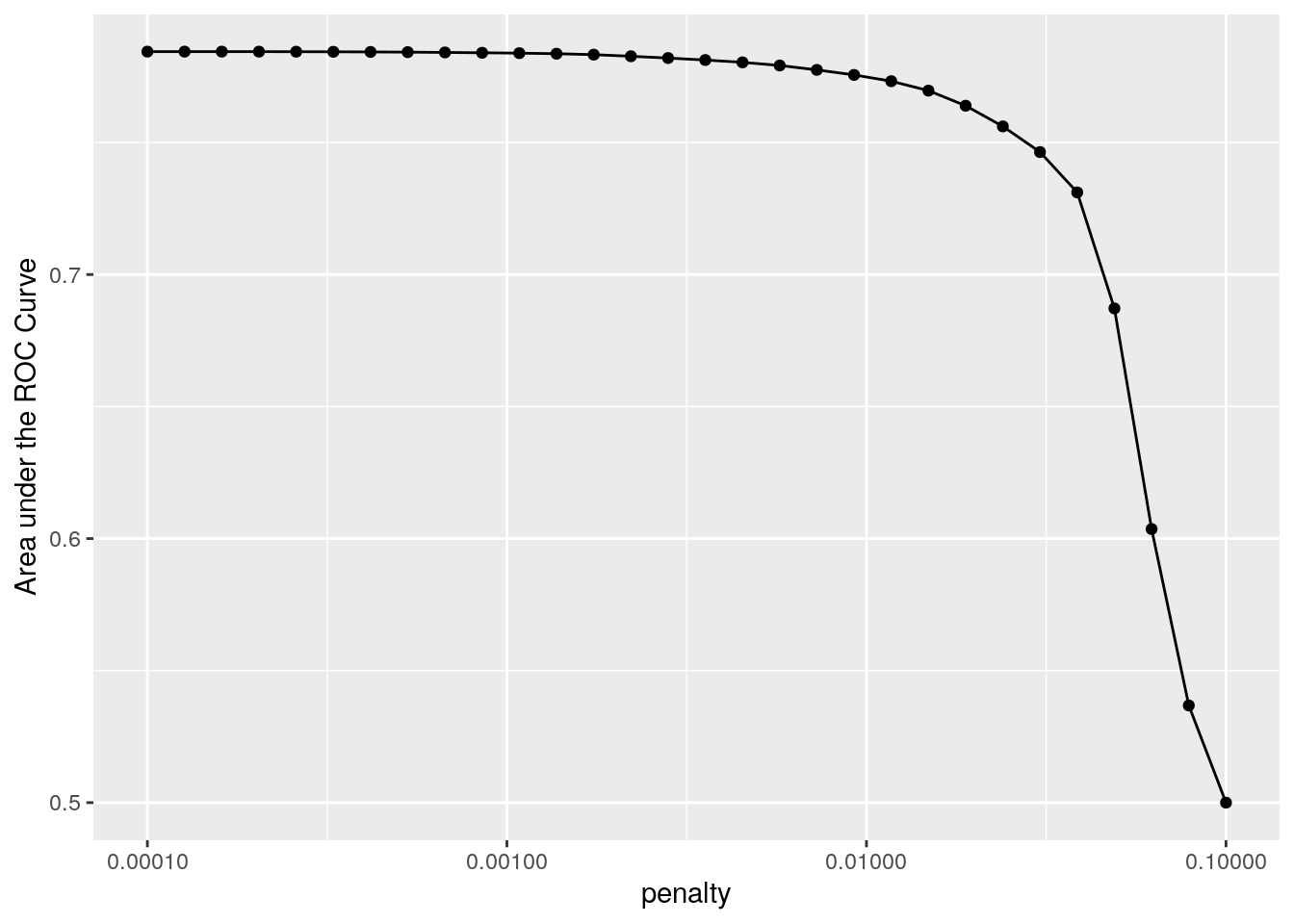
This plot suggests model performance is generally better at the smaller penalty values, meaning the majority of the predictors are important to the model. There’s also a steep drop in the area under the ROC curve towards the highest penalty values. This happens because a large enough penalty will remove all predictors from the model. And when there are no predictors in the model, predictive accuracy takes a nose dive.
Our model performance seems to plateau at the smaller penalty values, so judging performance by the roc_auc metric alone could lead to multiple options for the “best” value for this hyperparameter.
lr_res %>%
show_best("roc_auc", n = 15) %>%
arrange(penalty)
# A tibble: 15 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.0001 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model01
2 0.000127 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model02
3 0.000161 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model03
4 0.000204 roc_auc binary 0.784 5 0.000717 Preprocessor1_Model04
5 0.000259 roc_auc binary 0.784 5 0.000719 Preprocessor1_Model05
6 0.000329 roc_auc binary 0.784 5 0.000724 Preprocessor1_Model06
7 0.000418 roc_auc binary 0.784 5 0.000727 Preprocessor1_Model07
8 0.000530 roc_auc binary 0.784 5 0.000732 Preprocessor1_Model08
9 0.000672 roc_auc binary 0.784 5 0.000732 Preprocessor1_Model09
10 0.000853 roc_auc binary 0.784 5 0.000728 Preprocessor1_Model10
11 0.00108 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model11
12 0.00137 roc_auc binary 0.784 5 0.000694 Preprocessor1_Model12
13 0.00174 roc_auc binary 0.783 5 0.000670 Preprocessor1_Model13
14 0.00221 roc_auc binary 0.783 5 0.000638 Preprocessor1_Model14
15 0.00281 roc_auc binary 0.782 5 0.000621 Preprocessor1_Model15
However, we may want to choose a penalty value further along the x-axis, closer to where we start to see the decline in model performance. For example, candidate model 12 with a penalty value of 0.00137 has basically the same performance as the numerically best model (model 1). However, model 12 might eliminate more predictors than model 1, and generally speaking, fewer irrelevant predictors is better. So if model performance is about the same, we should choose a model with a higher penalty value.
But keep in mind, we also collected other performance metrics. So, let’s take a look at those:
perf_metrics <- c("roc_auc", "precision", "recall", "f_meas")
get_metrics <- function(x) {
lr_res %>%
show_best(x, n = 15) %>%
arrange(penalty)
}
map(perf_metrics, get_metrics)
[[1]]
# A tibble: 15 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.0001 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model01
2 0.000127 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model02
3 0.000161 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model03
4 0.000204 roc_auc binary 0.784 5 0.000717 Preprocessor1_Model04
5 0.000259 roc_auc binary 0.784 5 0.000719 Preprocessor1_Model05
6 0.000329 roc_auc binary 0.784 5 0.000724 Preprocessor1_Model06
7 0.000418 roc_auc binary 0.784 5 0.000727 Preprocessor1_Model07
8 0.000530 roc_auc binary 0.784 5 0.000732 Preprocessor1_Model08
9 0.000672 roc_auc binary 0.784 5 0.000732 Preprocessor1_Model09
10 0.000853 roc_auc binary 0.784 5 0.000728 Preprocessor1_Model10
11 0.00108 roc_auc binary 0.784 5 0.000715 Preprocessor1_Model11
12 0.00137 roc_auc binary 0.784 5 0.000694 Preprocessor1_Model12
13 0.00174 roc_auc binary 0.783 5 0.000670 Preprocessor1_Model13
14 0.00221 roc_auc binary 0.783 5 0.000638 Preprocessor1_Model14
15 0.00281 roc_auc binary 0.782 5 0.000621 Preprocessor1_Model15
[[2]]
# A tibble: 15 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.0001 precision binary 0.810 5 0.000335 Preprocessor1_Model01
2 0.000127 precision binary 0.810 5 0.000335 Preprocessor1_Model02
3 0.000161 precision binary 0.810 5 0.000335 Preprocessor1_Model03
4 0.000204 precision binary 0.810 5 0.000318 Preprocessor1_Model04
5 0.000259 precision binary 0.810 5 0.000304 Preprocessor1_Model05
6 0.000329 precision binary 0.809 5 0.000309 Preprocessor1_Model06
7 0.000418 precision binary 0.809 5 0.000309 Preprocessor1_Model07
8 0.000530 precision binary 0.809 5 0.000329 Preprocessor1_Model08
9 0.000672 precision binary 0.809 5 0.000339 Preprocessor1_Model09
10 0.000853 precision binary 0.808 5 0.000278 Preprocessor1_Model10
11 0.00108 precision binary 0.808 5 0.000251 Preprocessor1_Model11
12 0.00137 precision binary 0.807 5 0.000234 Preprocessor1_Model12
13 0.00174 precision binary 0.807 5 0.000218 Preprocessor1_Model13
14 0.00221 precision binary 0.806 5 0.000180 Preprocessor1_Model14
15 0.00281 precision binary 0.805 5 0.0000979 Preprocessor1_Model15
[[3]]
# A tibble: 15 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.00356 recall binary 0.956 5 0.000631 Preprocessor1_Model16
2 0.00452 recall binary 0.957 5 0.000670 Preprocessor1_Model17
3 0.00574 recall binary 0.960 5 0.000627 Preprocessor1_Model18
4 0.00728 recall binary 0.962 5 0.000723 Preprocessor1_Model19
5 0.00924 recall binary 0.967 5 0.000365 Preprocessor1_Model20
6 0.0117 recall binary 0.974 5 0.000515 Preprocessor1_Model21
7 0.0149 recall binary 0.981 5 0.000532 Preprocessor1_Model22
8 0.0189 recall binary 0.984 5 0.000379 Preprocessor1_Model23
9 0.0240 recall binary 0.990 5 0.000264 Preprocessor1_Model24
10 0.0304 recall binary 0.993 5 0.000201 Preprocessor1_Model25
11 0.0386 recall binary 0.996 5 0.000131 Preprocessor1_Model26
12 0.0489 recall binary 0.996 5 0.000162 Preprocessor1_Model27
13 0.0621 recall binary 1 5 0 Preprocessor1_Model28
14 0.0788 recall binary 1 5 0 Preprocessor1_Model29
15 0.1 recall binary 1 5 0 Preprocessor1_Model30
[[4]]
# A tibble: 15 × 7
penalty .metric .estimator mean n std_err .config
<dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
1 0.0001 f_meas binary 0.873 5 0.000454 Preprocessor1_Model01
2 0.000127 f_meas binary 0.873 5 0.000454 Preprocessor1_Model02
3 0.000161 f_meas binary 0.873 5 0.000454 Preprocessor1_Model03
4 0.000204 f_meas binary 0.873 5 0.000448 Preprocessor1_Model04
5 0.000259 f_meas binary 0.873 5 0.000421 Preprocessor1_Model05
6 0.000329 f_meas binary 0.873 5 0.000422 Preprocessor1_Model06
7 0.000530 f_meas binary 0.873 5 0.000437 Preprocessor1_Model08
8 0.000672 f_meas binary 0.873 5 0.000428 Preprocessor1_Model09
9 0.000853 f_meas binary 0.873 5 0.000400 Preprocessor1_Model10
10 0.00108 f_meas binary 0.873 5 0.000371 Preprocessor1_Model11
11 0.00137 f_meas binary 0.873 5 0.000354 Preprocessor1_Model12
12 0.00174 f_meas binary 0.873 5 0.000377 Preprocessor1_Model13
13 0.00221 f_meas binary 0.873 5 0.000326 Preprocessor1_Model14
14 0.00281 f_meas binary 0.873 5 0.000299 Preprocessor1_Model15
15 0.00356 f_meas binary 0.873 5 0.000266 Preprocessor1_Model16
Let’s select model 15 in this case:
lr_best <- lr_res %>%
select_best(metric = "f_meas")
Now we can use the predictions to create a confusion matrix with conf_mat().
lr_res %>%
collect_predictions(parameters = lr_best) %>%
conf_mat(crash_type, .pred_class)
Truth
Prediction no injury / drive away
no injury / drive away 303912
injury and / or tow due to crash 14507
Truth
Prediction injury and / or tow due to crash
no injury / drive away 73671
injury and / or tow due to crash 36297
The confusion matrix can also be visualized in different formats using autoplot(). I personally like the heatmap type, but there are others that can be used as well.
lr_res %>%
collect_predictions(parameters = lr_best) %>%
conf_mat(crash_type, .pred_class) %>%
autoplot(type = "heatmap")

Let’s visualize the validation set ROC curve:
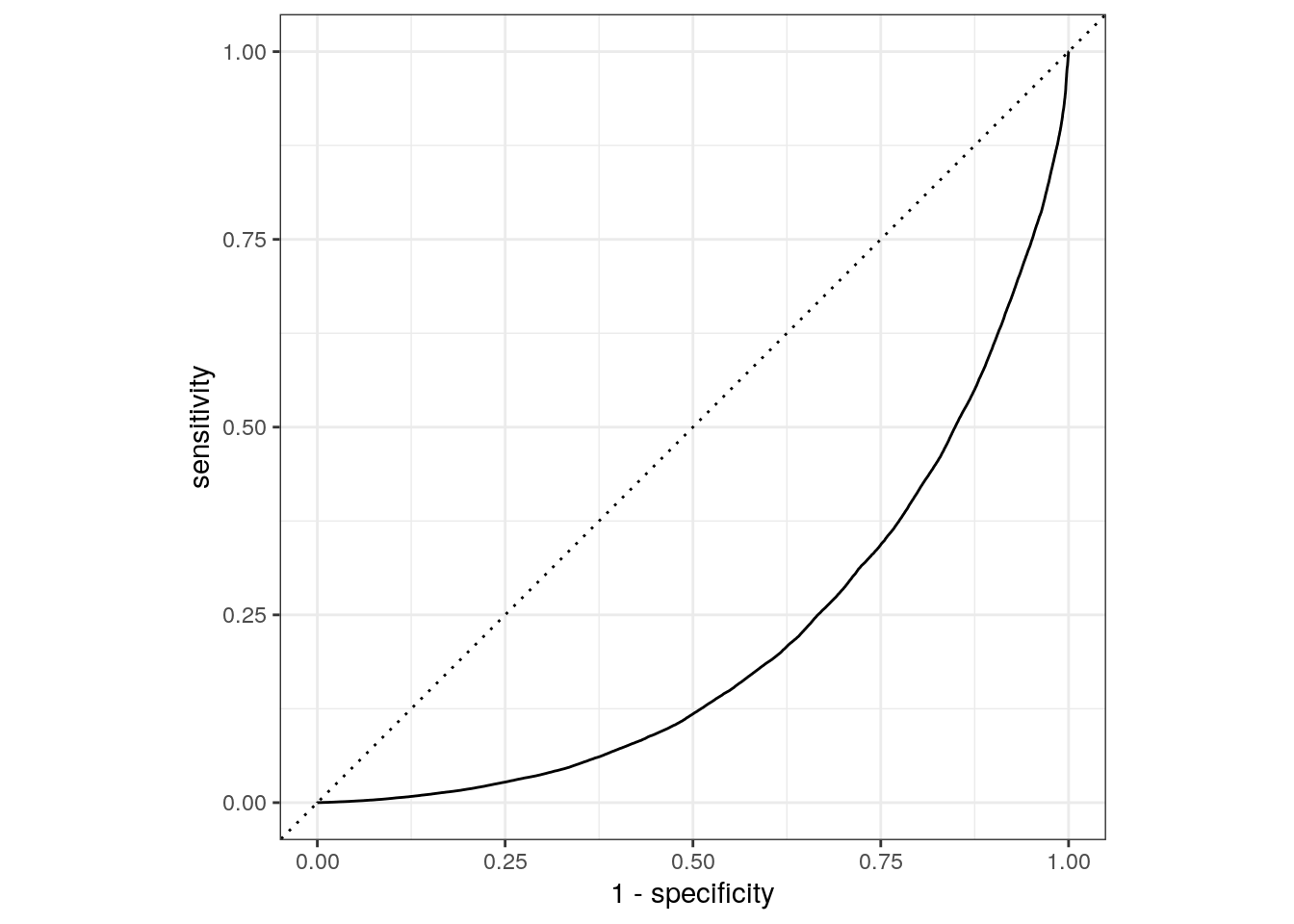
lr_auc <- lr_res %>%
collect_predictions(parameters = lr_best) %>%
roc_curve(crash_type, `.pred_injury and / or tow due to crash`) %>%
mutate(model = "Logistic Regression")
autoplot(lr_auc)
We can also make a ROC cure for the 5 folds. Since the category we are predicting is the injury/tow level in the crash_type factor, we provide roc_curve() with the relevant class probability .pred_injury and / or tow due to crash:
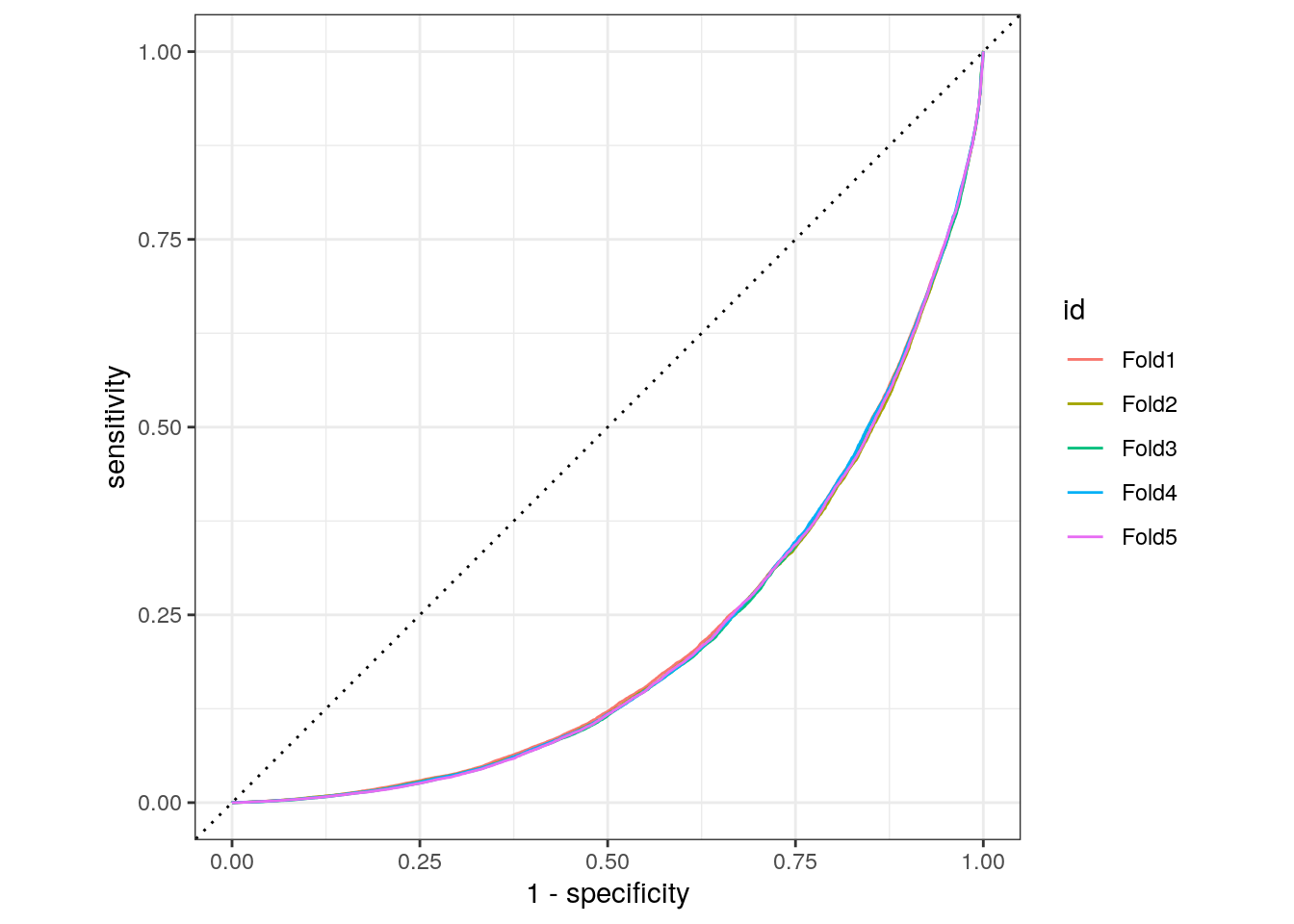
lr_res %>%
collect_predictions(parameters = lr_best) %>%
group_by(id) %>%
roc_curve(crash_type, `.pred_injury and / or tow due to crash`) %>%
autoplot()
Finally, we can also look at the predicted probability distributions for our two classes:
lr_res %>%
collect_predictions(parameters = lr_best) %>%
ggplot() +
geom_density(
aes(x = `.pred_injury and / or tow due to crash`,
fill = crash_type),
alpha = 0.5
)
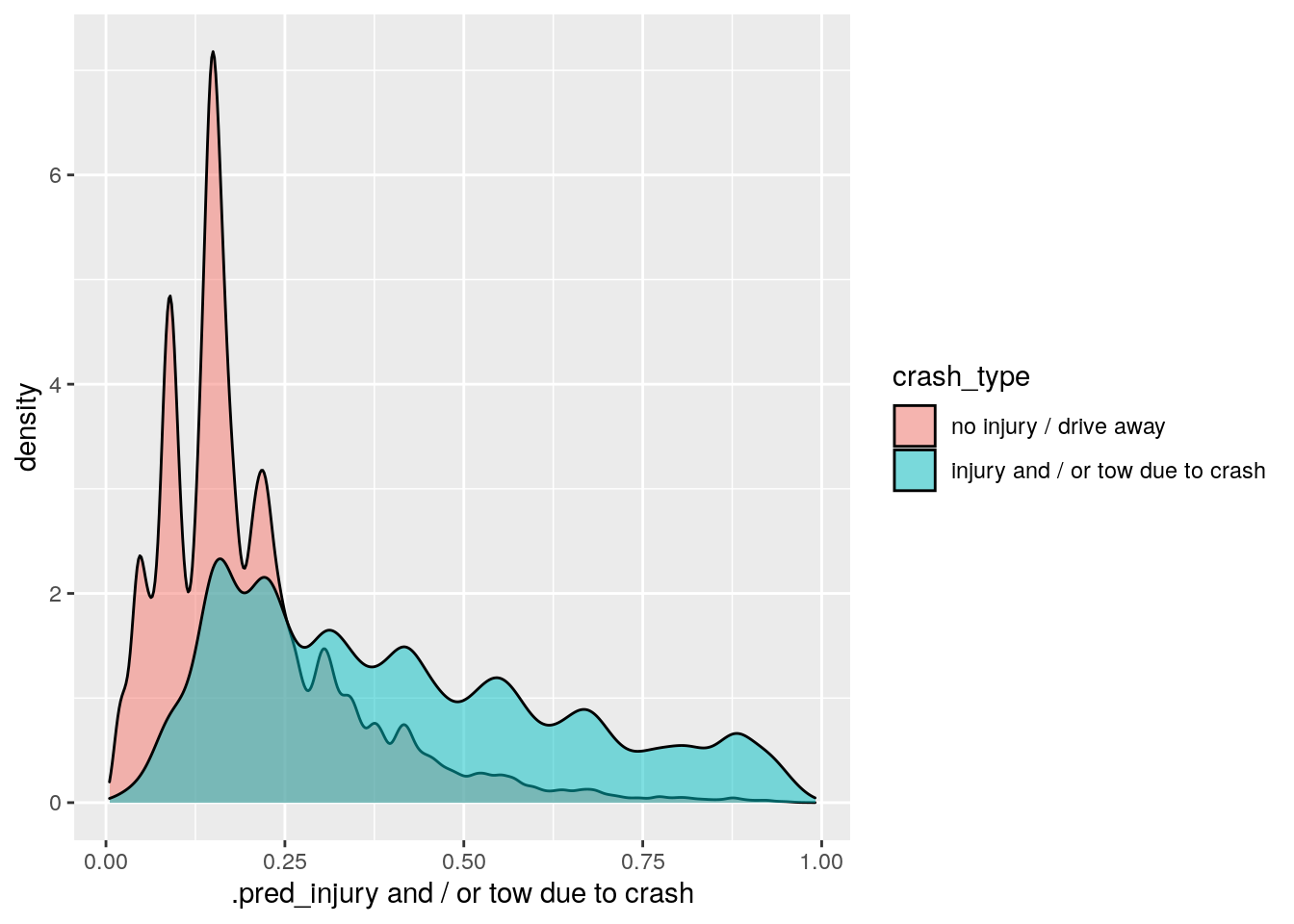
The level of performance generated by this logistic regression model isn’t great, but it’s better than an educated guess. Based on the frequency of crashes that result in injuries or vehicles being towed in the entire data set, we would expect about 24.6% of crashes to have these outcomes. However, based on the features we’ve selected here, our model correctly predicted these crash types about 33% of the time. So, we’ve improved our predictions, but only by about 8%. Perhaps the linear nature of the prediction equation could be limiting our model’s performance. As a next step, we might consider using a non-linear model, like a tree-based ensemble method.
Model 2: Random forest
An effective, low-maintenance, non-linear modeling approach is a random forest, which tends to be more flexible than logistic regression. A random forest is an ensemble model that often consists of thousands of decision trees. Each individual tree sees a slightly different version of the training set and learns a sequence of splitting rules to predict new data. Random forests require very little preprocessing and can handle many types of predictors (e.g., skewed, continuous, categorical, etc.). Although the default hyperparameters for random forests tend to give reasonable results, we’ll tune two hyperparameters that could improve performance. This should also help since we’ll be limiting the number of trees used to 20 to speed up the time it takes to fit the model.
rf_mod <- rand_forest(mtry = tune(), min_n = tune(), trees = 20) %>%
set_engine("ranger", importance = "impurity") %>%
set_mode("classification")
For the hyperparameters in this model, we use tune() as a placeholder for the mtry and min_n argument values. The mtry hyperparameter sets the number of predictor variables that each node in the decision tree sees and learns about. The min_n hyperparameter sets the minimum n to split at any node. We also added importance = "impurity" when setting the engine. This will provide variable importance scores for this model, which gives some insight into which predictors drive model performance.
Create the workflow
Next, let’s bundle the recipe and model.
rf_workflow <- workflow() %>%
add_model(rf_mod) %>%
add_recipe(crash_recipe)
Train and tune the model
Since we have more than one hyperparameter to tune in this model, let’s use a space-filling design with 25 candidate models.
rf_res <- rf_workflow %>%
tune_grid(
crashes_vfold,
grid = 25,
control = control_grid(save_pred = TRUE),
metrics = metric_set(roc_auc, precision, recall, f_meas)
)
i Creating pre-processing data to finalize unknown parameter: mtry
Evaluate the model
Out of the 25 candidates, here are the top 5 random forest models based on their F1-Scores:
rf_res %>%
show_best(metric = "f_meas")
# A tibble: 5 × 8
mtry min_n .metric .estimator mean n std_err .config
<int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
1 6 19 f_meas binary 0.874 5 0.000433 Preprocessor1_Model20
2 5 27 f_meas binary 0.874 5 0.000388 Preprocessor1_Model03
3 16 31 f_meas binary 0.872 5 0.000379 Preprocessor1_Model24
4 22 39 f_meas binary 0.872 5 0.000454 Preprocessor1_Model10
5 13 7 f_meas binary 0.871 5 0.000403 Preprocessor1_Model16
Let’s select the best model according to the F1-Score. Our final tuning parameter values are:
rf_best <- rf_res %>%
select_best(metric = "f_meas")
rf_best
# A tibble: 1 × 3
mtry min_n .config
<int> <int> <chr>
1 6 19 Preprocessor1_Model20
To calculate the data needed to plot the ROC curve, we use collect_predictions(). This is only possible after tuning with control_grid(save_pred = TRUE). Now, we can use the predictions to create a confusion matrix with conf_mat().
rf_res %>%
collect_predictions() %>%
conf_mat(crash_type, .pred_class)
Truth
Prediction no injury / drive away
no injury / drive away 7349427
injury and / or tow due to crash 611048
Truth
Prediction injury and / or tow due to crash
no injury / drive away 1662563
injury and / or tow due to crash 1086637
To filter the predictions for only our best random forest model, we can use the parameters argument and pass it our tibble with the best hyperparameter values from tuning, which we called rf_best.
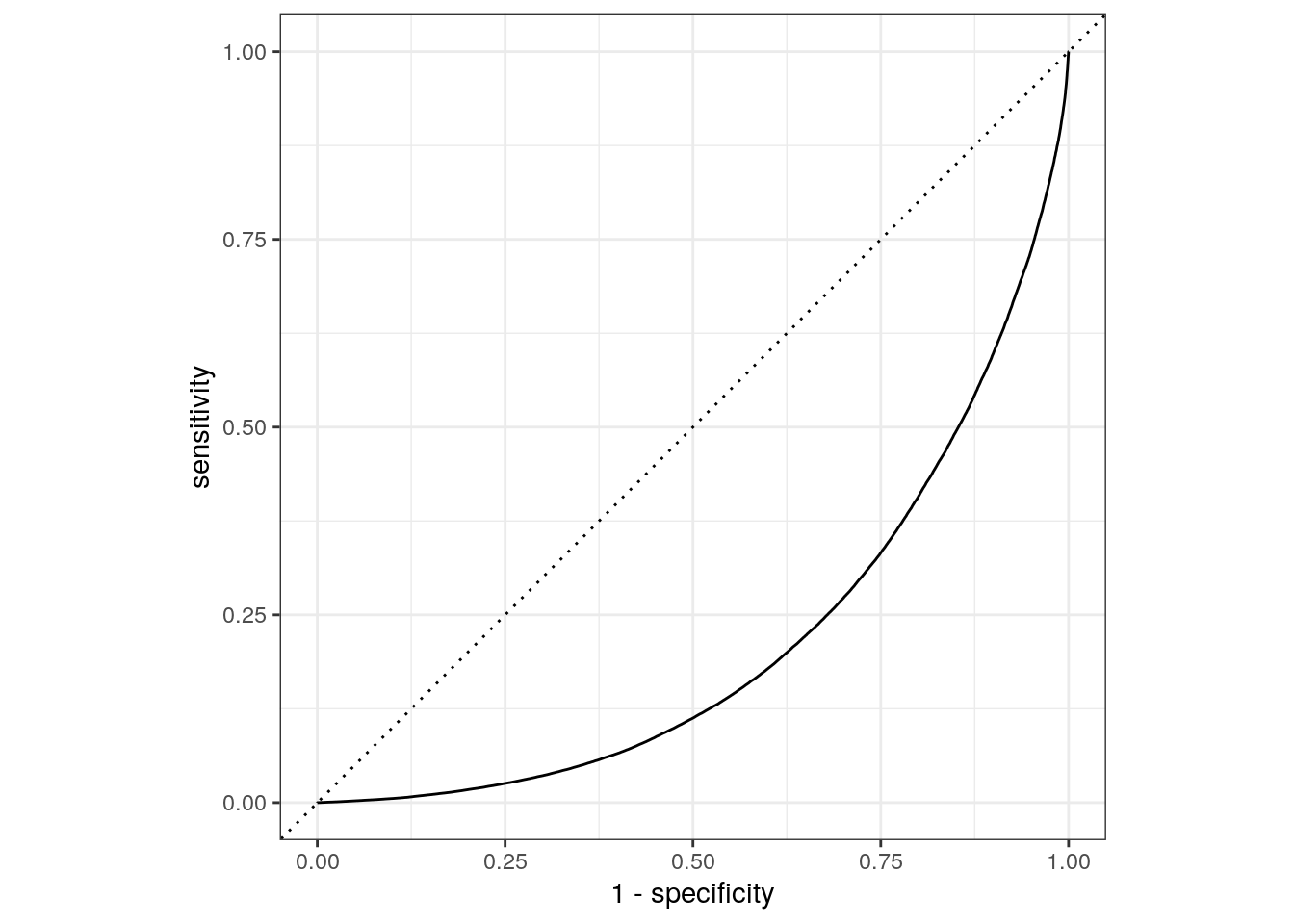
rf_auc <- rf_res %>%
collect_predictions(parameters = rf_best) %>%
roc_curve(crash_type, `.pred_injury and / or tow due to crash`) %>%
mutate(model = "Random Forest")
autoplot(rf_auc)
Compare models
Now, it’s time to compare the models. The first thing we’ll do is extract the performance metrics from each of the models and combine them into a single data frame.
lr_metrics <- lr_res %>%
collect_metrics() %>%
mutate(model = "Logistic Regression")
rf_metrics <- rf_res %>%
collect_metrics() %>%
mutate(model = "Random Forest")
compare_mod <- bind_rows(lr_metrics, rf_metrics)
Fist, let’s take a look at the average F1-Score for each model:
compare_mod %>%
filter(.metric == "f_meas") %>%
group_by(model) %>%
summarize(avg_f_meas = mean(mean)) %>%
mutate(model = fct_reorder(model, avg_f_meas)) %>%
ggplot(aes(model, avg_f_meas, fill = model)) +
geom_col() +
coord_flip() +
scale_fill_brewer(palette = "Blues") +
geom_text(
size = 5,
aes(label = round_half_up(avg_f_meas, 2), y = avg_f_meas - .8)
)
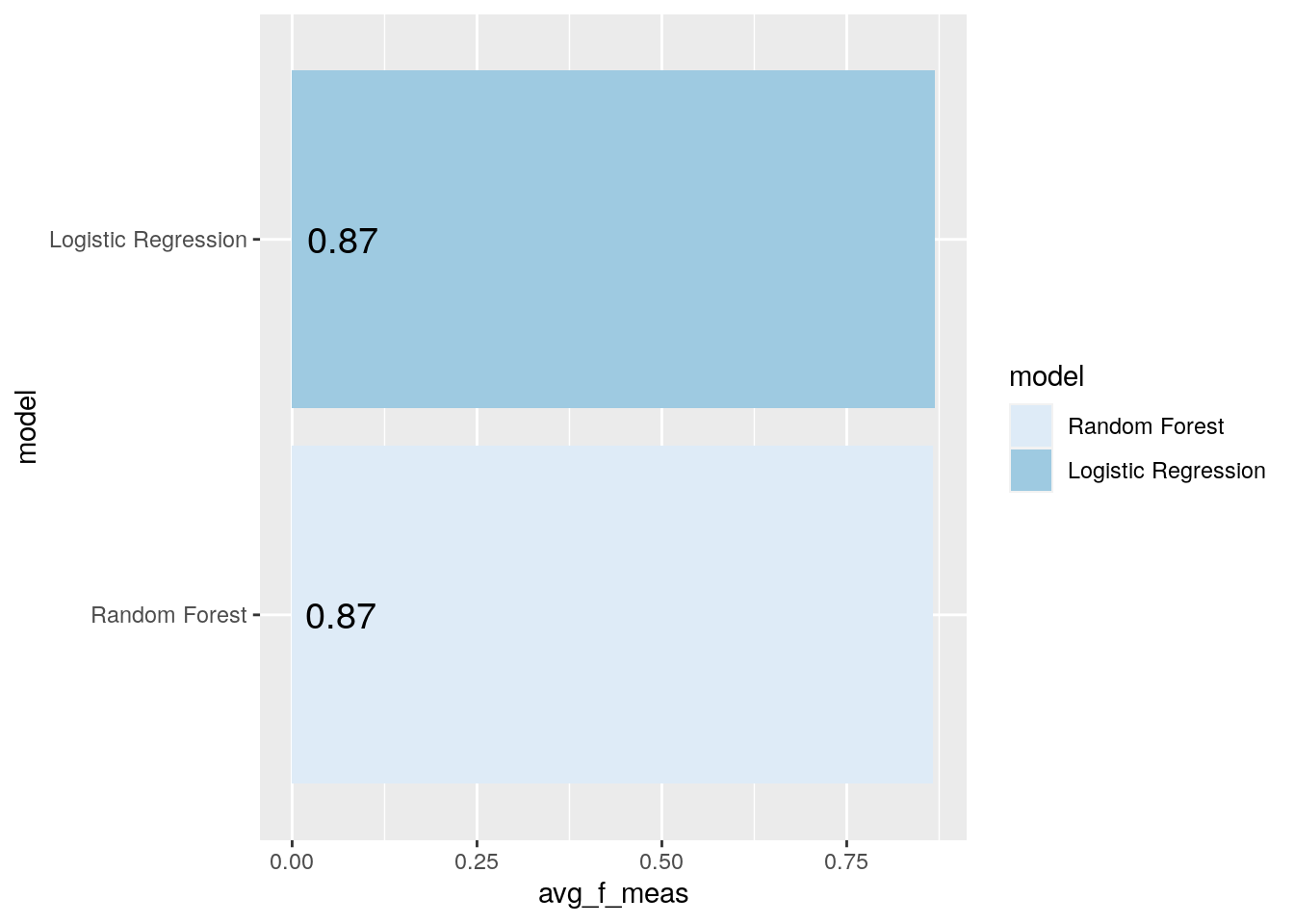
Not much of a difference here. So, we may also want to check out the average ROC curve for each model:
compare_mod %>%
filter(.metric == "roc_auc") %>%
group_by(model) %>%
summarize(avg_roc = mean(mean)) %>%
mutate(model = fct_reorder(model, avg_roc)) %>%
ggplot(aes(model, avg_roc, fill = model)) +
geom_col() +
coord_flip() +
scale_fill_brewer(palette = "Blues") +
geom_text(
size = 5,
aes(label = round_half_up(avg_roc, 2), y = avg_roc - .7)
)
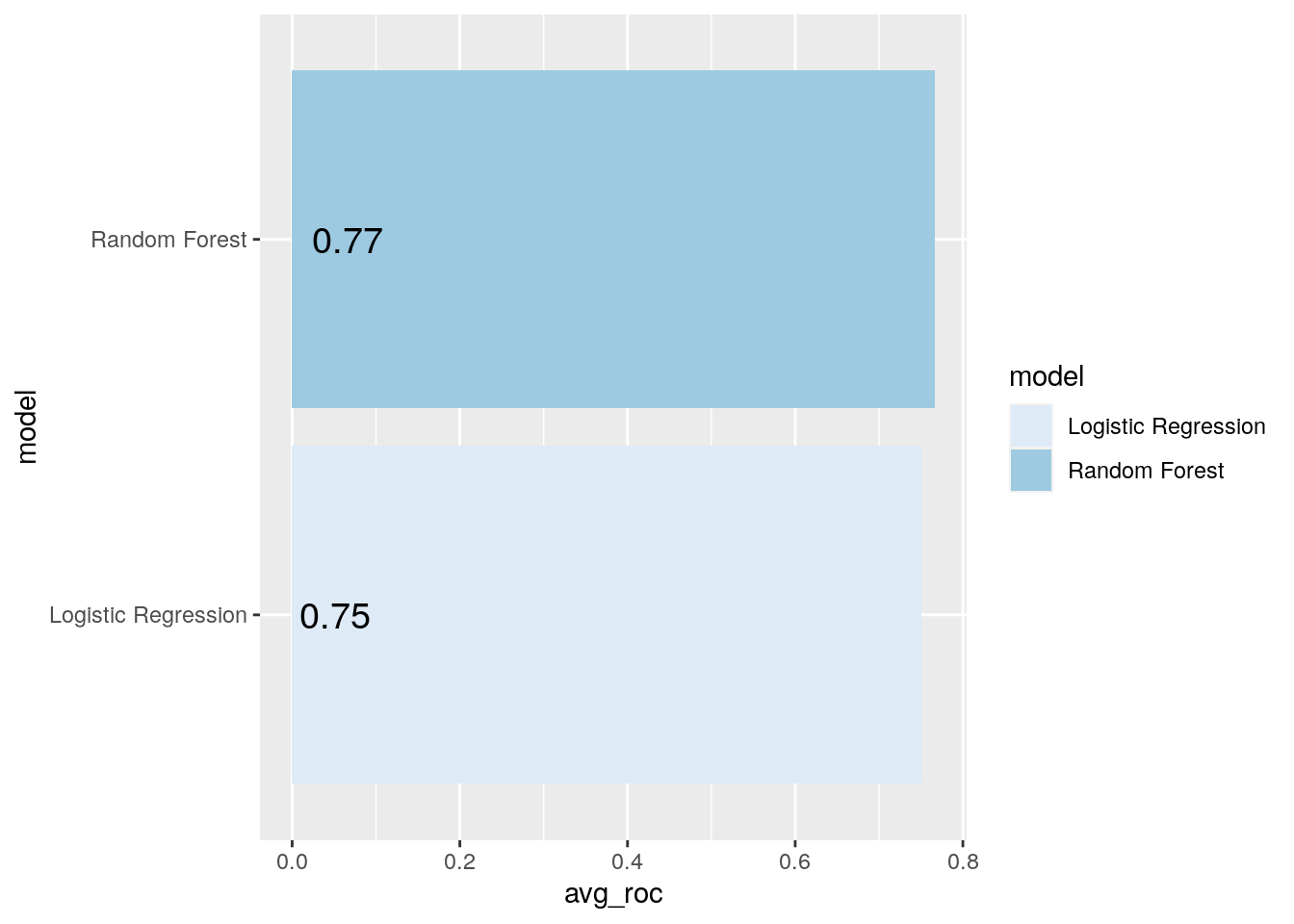
Looks like our random forest model did a bit better here, but still pretty close. Let’s plot the validation set ROC curves for the top penalized logistic regression model and random forest model:
bind_rows(rf_auc, lr_auc) %>%
ggplot(aes(x = 1 - specificity, y = sensitivity, col = model)) +
geom_path(lwd = 1.5, alpha = 0.8) +
geom_abline(lty = 3) +
coord_equal() +
scale_color_viridis_d(option = "plasma", end = .6)
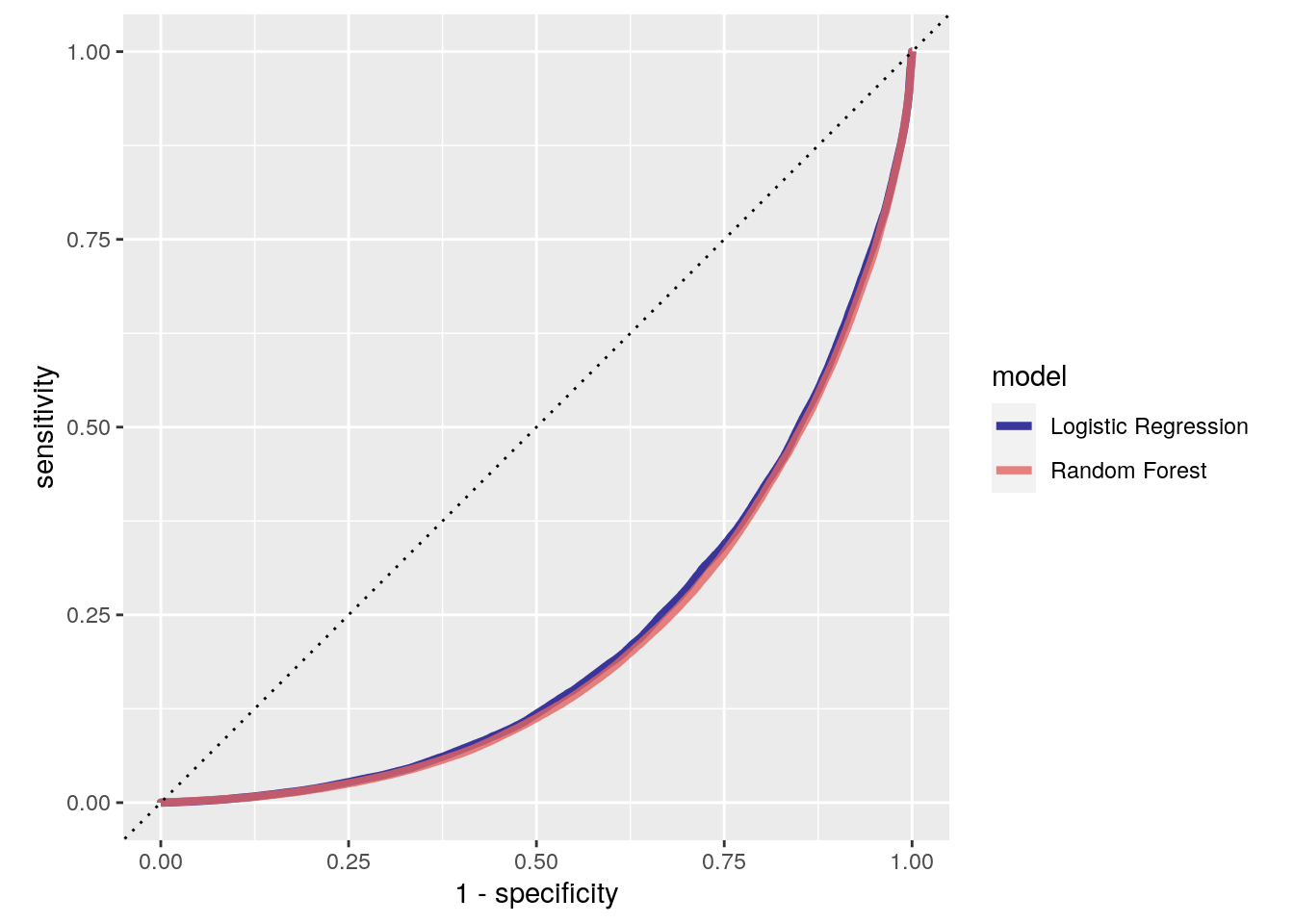
Overall, the model results are pretty similar, but the random forest model did seem to perform better than the logistic regression model. In this case, I highlighted the ROC AUC and F1-Score performance metrics, but the “best” performance metric will always depend on the question you are trying to answer with your model. For example, in some cases, you might be much more concerned about false negatives than you are false positives (e.g., when predicting severe storms). In other situations, you might only be concerned about each these to the extent they influence a model’s precision (e.g., when predicting profitable stocks).
To keep things simple, let’s stick with the ROC AUC metric in this case. AUC stands for area under the curve. What curve, you may ask? The ROC curve, specifically. The ROC curve plots the tradeoff between the true positive rate (sensitivity) and and false positive rate (1 - specificity). Ideally, we want to maximize the true positive rate and minimize the false positive rate.
Let’s find the maximum mean ROC AUC:
compare_mod %>%
filter(.metric == "roc_auc") %>%
group_by(model) %>%
summarize(avg_roc_auc = mean(mean)) %>%
slice_max(avg_roc_auc)
[38;5;246m# A tibble: 1 × 2[39m
model avg_roc_auc
[3m[38;5;246m<chr>[39m[23m [3m[38;5;246m<dbl>[39m[23m
[38;5;250m1[39m Random Forest 0.766
Now, it’s time to fit the best model one last time to the full training set. Then, we can evaluate the resulting final model on the test set.
Last fit
Recall that our goal was to predict whether a traffic crash would result in an injury or a vehicle being towed based on a priori situational factors. Given the results, we determined the random forest model performed better than the penalized logistic regression model. We also know learned the best model hyperparameters from the rf_best object we created earlier. Now, we just need to fit the final model on all the rows of data not originally held out for testing (i.e., the training and validation sets) and evaluate the model performance one more time with the test set.
The
tune package contains the function last_fit(), which fits a model to the whole training data and evaluates it on the test set. We just need to provide the workflow object of the best model and data split object (not the training data).
last_rf_mod <- rand_forest(
mtry = rf_best$mtry,
min_n = rf_best$min_n,
trees = 20
) %>%
set_engine("ranger", importance = "impurity") %>%
set_mode("classification")
last_rf_workflow <- rf_workflow %>%
update_model(last_rf_mod)
last_rf_fit <- last_rf_workflow %>%
last_fit(crash_split)
And these are the final performance metrics:
last_rf_fit %>%
collect_metrics()
[38;5;246m# A tibble: 2 × 4[39m
.metric .estimator .estimate .config
[3m[38;5;246m<chr>[39m[23m [3m[38;5;246m<chr>[39m[23m [3m[38;5;246m<dbl>[39m[23m [3m[38;5;246m<chr>[39m[23m
[38;5;250m1[39m accuracy binary 0.795 Preprocessor1_Model1
[38;5;250m2[39m roc_auc binary 0.787 Preprocessor1_Model1
Remember, if a model fit to the training data set also fits the test data set well, we can be reasonably confident that minimal overfitting has taken place.
To learn more about the model, we can look at the variable importance scores in the .workflow column. We pluck the first element from the column, and pull out the fit from the workflow object. Then, we can use the
vip package to visualize the variable importance scores for the top features.
last_rf_fit %>%
pluck(".workflow", 1) %>%
extract_fit_parsnip() %>%
vip(num_features = 10)
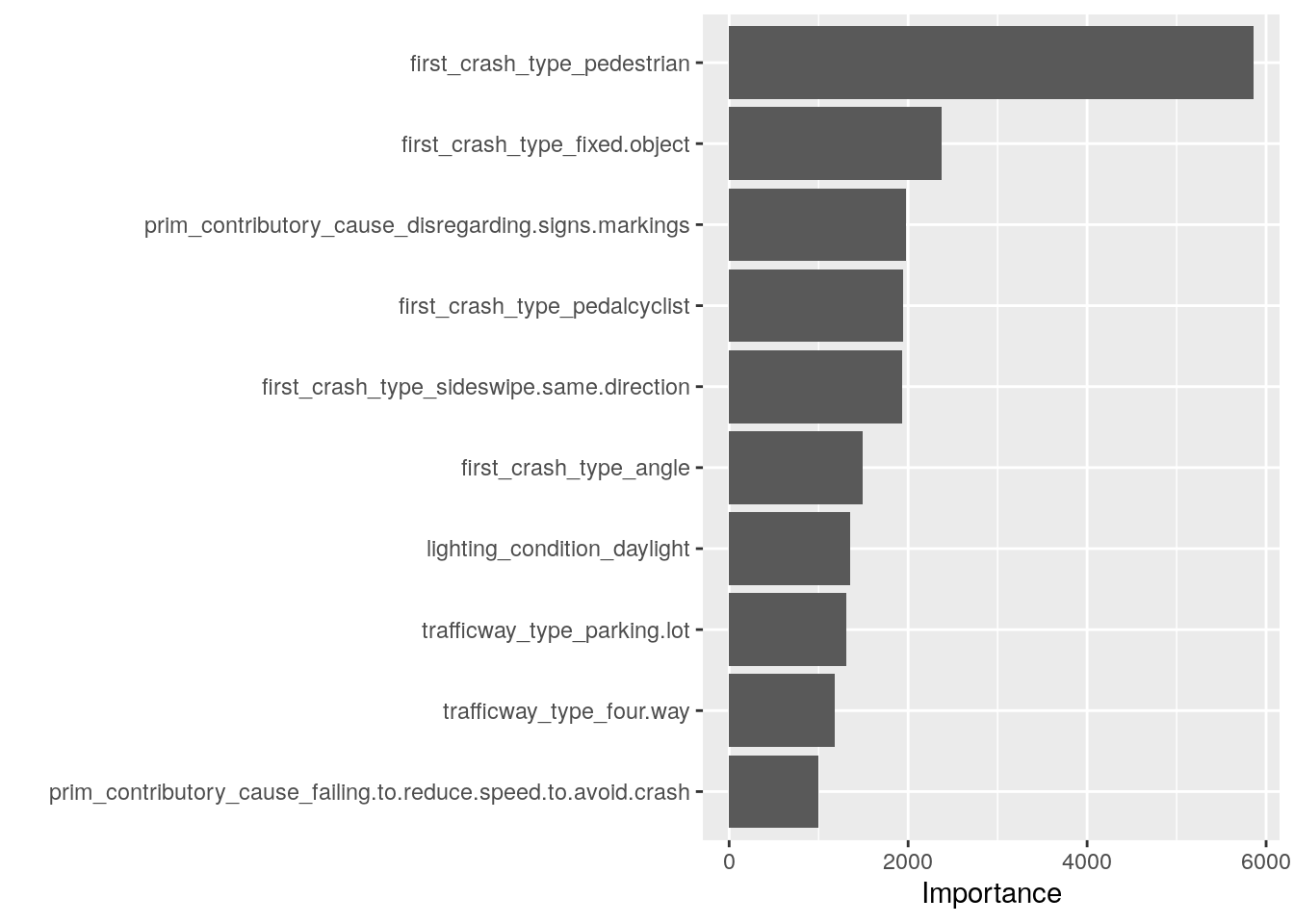
By far, the most important factor in whether a crash results in injuries or the vehicle being towed is if the first collision in the crash involved a pedestrian or not.
Let’s take a quick look at the confusion matrix:
last_rf_fit %>%
collect_predictions() %>%
conf_mat(crash_type, .pred_class) %>%
autoplot(type = "heatmap")
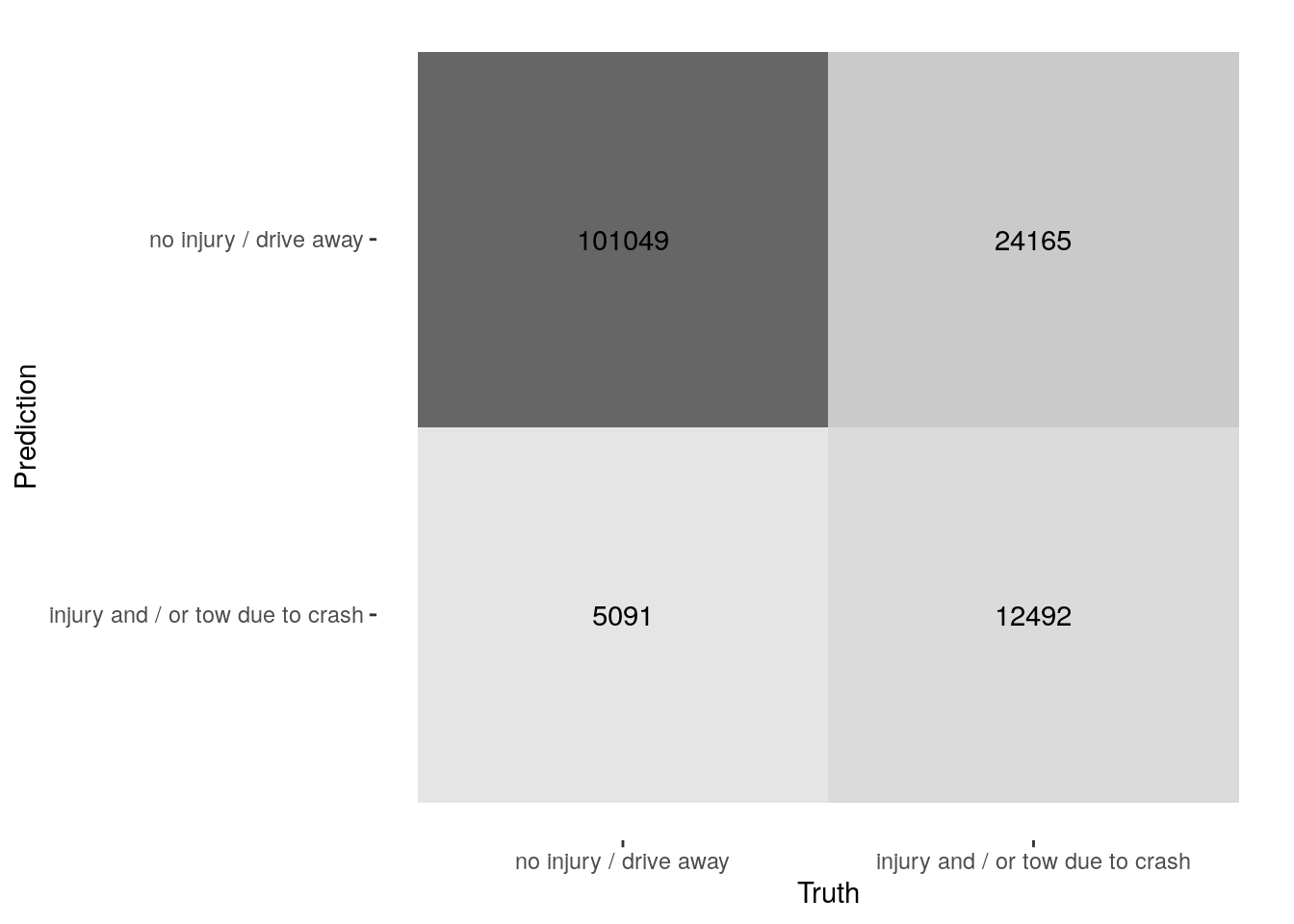
And, let’s create the final ROC curve:
last_rf_fit %>%
collect_predictions() %>%
roc_curve(crash_type, `.pred_injury and / or tow due to crash`) %>%
autoplot()
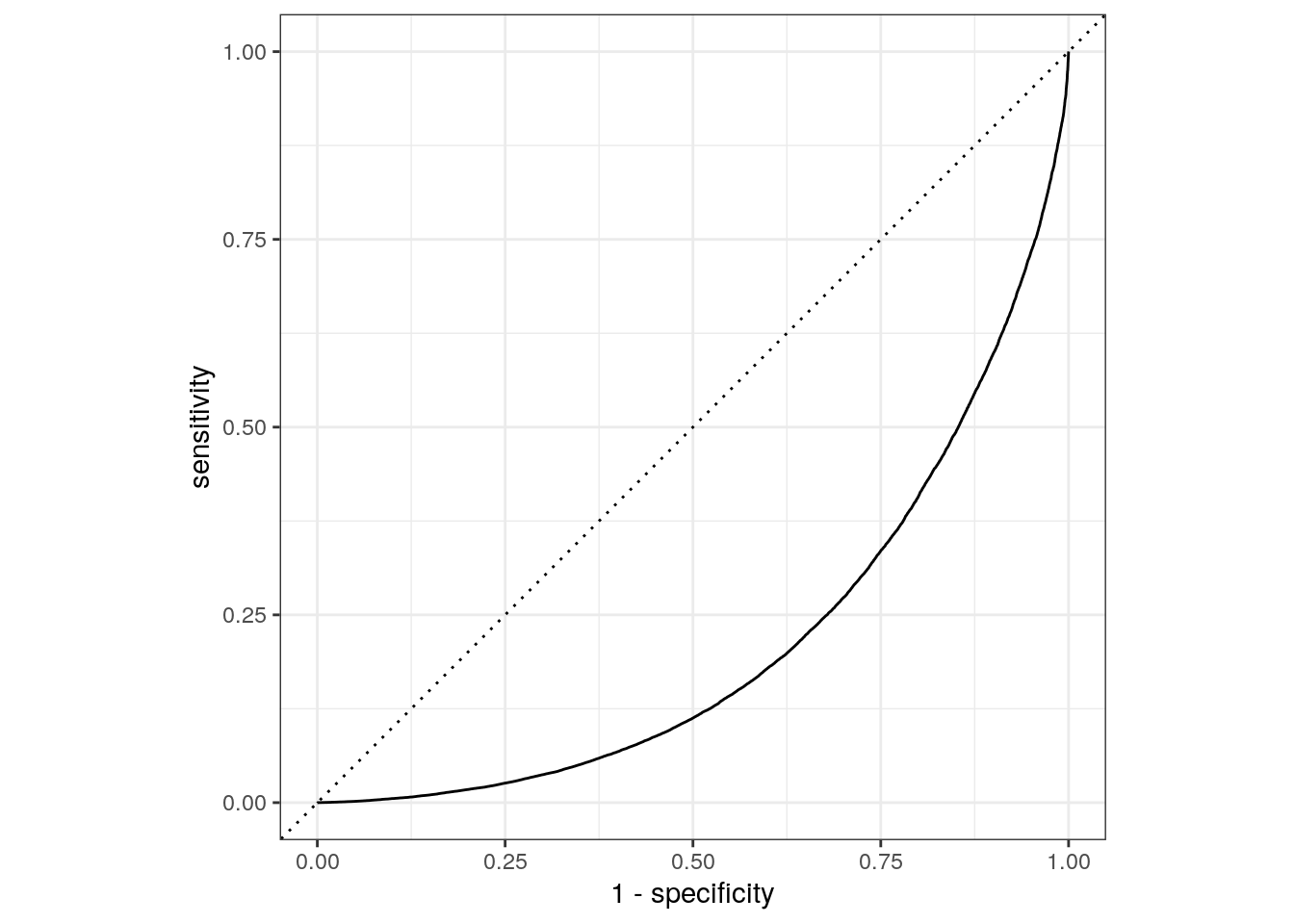
The results from the validation set and test set performance statistics are very close, so we can be reasonably confident the random forest model with the selected features and hyperparameters would perform well when predicting new data.
Special thanks to Drew Triplett for his helpful comments on an earlier draft of this post!